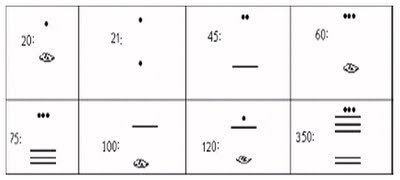
O sistema de numeração de base dois é o sistema que emprega a menor base numérica possível para o sistema de numeração posicional .
É fácil perceber que uma base numérica menor que dois é inviável tanto do ponto de vista prático como do ponto de vista matemático. Uma base negativa é impensável, pois os números negativos sequer eram trabalhados nos tempos em que se solidificou o sistema de numeração posicional na história da matemática. Mesmo hoje, quando se tem uma noção perfeitamente compreensível dos números negativos, a idéia de se estipular uma base numérica menor que zero é descartada pelo fato de que, com isso, iria se priorizar os cálculos de números negativos e é claro que os números positivos maiores que zero são mais utilizados na prática que os números negativos, embora do ponto de vista matemático uma base numérica negativa é perfeitamente aceitável.
O zero e o um seguramente não podem ser tomados como bases numéricas. Quando temos a base dez, necessitamos de dez símbolos diferentes para representarmos os algarismos, quando temos a base cinco, cinco símbolos, a base três, três símbolos e assim por diante. Portanto, a base zero não teria símbolo algum e a base um teria somente o zero como símbolo, ou seja, é impossível estipular como base numérica o número zero ou o número um. Portanto, como a base dois é a menor base numérica do sistema de numeração posicional, é também o sistema de numeração mais simples que existe, pois somente utilizando os números 0 e 1. Este sistema de numeração binário é um dos sistemas mais antigos que se conhece provavelmente devido à sua simplicidade. Alguns povos da Austrália e da Polinésia já usavam, apesar de com certa imperfeição, esse sistema de numeração posicional de base dois.
No século XVII, esse sistema de numeração foi proposto por um grande matemático alemão chamado Gottfried Wilhelm Leibniz (1646-1716) numa época que se discutia qual era a base de numeração mais eficiente. Note que não é apenas a representação dos algarismos que é simplificada no sistema de numeração binário. As regras das operações nesse sistema são extremamente simples, veja a adição e multiplicação no sistema de numeração binária:
O sistema de numeração binário é aquele de base numérica dois. Teremos, portanto, que utilizar apenas dois dígitos diferentes para representar seus algarismos: 0 e 1, com 1 > 0.
O sistema de numeração binário tem uma desvantagem em comparação com os demais sistemas numéricos: a enorme quantidade de dígitos que temos que empregar para realizar a notação de números relativamente grandes. Como a representação binária é bastante simples, esse sistema possibilita sua utilização em códigos, relacionando letras e números. Assim:
_-0, A-1, B-2, C-3, D-4, E-5, F-6, G-7, H-8, I-9, J-10, K-1, L-12, M-13, N-14, O-15, P-16, Q-17, R-18, S-19, T-20, U-21, V-22, W-23, X-24, Y-25, Z-26.
Como 25=32, cada letra será representada por cinco dígitos.
_-00000, A-00001, B-00010,..., Z-11010.
Este código que acabamos de colocar pode ser usado num aparelho de telegrafia. Supondo que temos dois locais unidos por cinco cabos de transmissão.Todas as letras do alfabeto podem ser transmitidas com o uso desses cinco cabos através de impulsos elétricos. Considerando que a ausência de impulso corresponde ao número zero, a existência do impulso ao número um e cada um dos cabos à um dígito do algarismo no sistema binário, pode-se converter a combinação de impulsos (um número do sistema binário) em letras do alfabeto, no local de recepção da mensagem. Esse processo é realizado com o auxílio de dois aparelhos: um transmissor capaz de converter letras em uma combinação de impulsos elétricos e um receptor capaz de realizar o processo inverso. É claro também que isso apenas é possível graças à facilidade em se converter um número no sistema binário em impulsos elétricos. Além do aparelho telegráfico, temos um outro aparelho que utiliza o sistema binário de numeração para realizar suas funções: as máquinas eletrônicas de somar, como computadores e calculadoras. Justamente por uma representação simples esse sistema é utilizado por essas máquinas que podem representar os números através não de impulsos elétricos como as telegráficas, mas através de semicondutores, porém, com o mesmo princípio de “sim” e “não” utilizado com os impulsos. Logicamente, os dados de um problema a ser resolvido por um computador são dados no sistema decimal de numeração e por isso a máquina necessita converter o número para o sistema binário. Essa tradução pode ser facilmente automatizada com a utilização de um sistema intermediário, ou seja, um sistema binário-decimal, por exemplo. Esse sistema consiste em traduzir cada dígito do número no sistema decimal para o sistema binário. Dessa forma, o número 2593 seria escrito como: 0010 0101 1001 0011.
Podemos entender como se realiza a adição em um computador que utiliza o sistema binário de numeração dessa forma: considere a o dígito de um dos números somados, b o dígito correspondente do segundo número somado, c um dígito que foi passado de uma ordem anterior (onde já foi realizada a soma) para a ordem da soma de a com b, r o dígito que deve ser escrito na ordem da soma de a com b e s o dígito que deve ser passado à ordem seguinte.
Todas as combinações (em cada coluna) de a, b, c, r, s, podem ser resumidas na tabela:

Para que o computador possa somar números escritos no sistema binário é necessário um dispositivo composto de três entradas, que correspondem aos dígitos a, b e c, e de duas saídas, que correspondem aos dígitos c e d. O número um corresponde à existência de corrente numa entrada ou numa saída e o zero corresponde à ausência de corrente. Este dispositivo é denominado somador de ordem e funciona de acordo com a tabela acima, ou seja, se não existir corrente em nenhuma das três entradas, tampouco existirá nas saídas, se existir corrente na entrada a, mas não existir nas entradas b e c, existirá corrente na saída r, mas não existirá na saída s, e assim por diante. É fácil, utilizando semicondutores, construir um dispositivo que funcione segundo esse esquema. Uma utilização bem interessante do sistema de numeração binária e dos códigos que podem ser realizados com esse tipo de sistema foi feita em 1969, quando o homem pisava na Lua pela primeira vez. Armstrong enviou uma mensagem para a Terra que depois de codificada ficou assim:

Cada bloco de oito dígitos equivale a um byte e cada dígito, a um bit.
Um byte representa uma letra, um sinal ou um número, utilizando a linguagem de computador.
A mensagem de Armstrong é traduzida assim:
“That’s one small step for a man, one giant leap for mankind.” _ Neil
“Este é um pequeno passo para um homem, mas um gigantesco salto para a humanidade.” _ Neil Armstrong, Apollo 11
O sistema de numeração binária funciona de acordo com um dispositivo bastante curioso, que é construído com várias lâmpadas, postas lado a lado. Este dispositivo funciona da seguinte forma:
- a seqüência das lâmpadas é o da direita para a esquerda;
- acionar uma lâmpada é equivalente a acendê-la, se estiver apagada, ou apagá-la, caso esteja acesa;
- quando uma lâmpada se apaga, a lâmpada imediatamente à sua esquerda se aciona;
- apenas a primeira lâmpada é acionada manualmente.
Conhecido o funcionamento do dispositivo, vamos atribuir valores para o estado da lâmpada. Uma lâmpada acesa equivale ao número um e uma lâmpada apagada equivale ao número zero.
Iniciando o processo com todas as lâmpadas apagadas, acionamos a primeira lâmpada. Temos o primeiro número do sistema binário de numeração. O segundo acionamento nos mostra o segundo número do sistema binário, o terceiro acionamento nos mostra o terceiro número e assim sucessivamente.
Veja um esquema do dispositivo:
Temos: lâmpada acesa (1) e lâmpada apagada (0). No primeiro acionamento acendemos a primeira lâmpada, ao apagá-la no segundo acionamento, a segunda lâmpada foi acionada. No terceiro acionamento, acendemos a primeira lâmpada, e assim por diante.
Ler mais...